Shame on you, R... again! (But not really...)

Remember how a few months ago I lamented the fact that the round() function in R uses a non-standard rule for rounding to the nearest integer?  Instead of rounding k+0.5 to k+1 (k being an integer) R rounds to whichever integer k or k+1 is even.  Well here's another example of R offending our mathematical sensibilities... R seems to think that even though

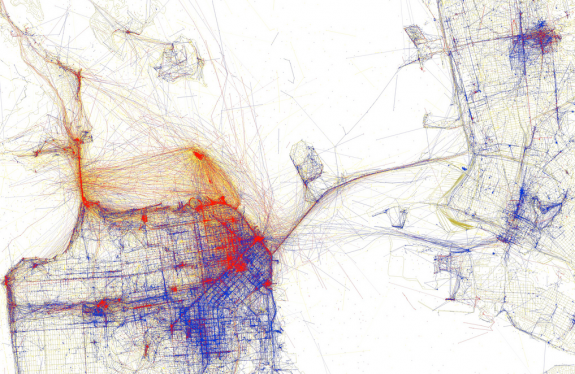
1 * Inf = Inf

somehow it can get away with telling us that

1 * (Inf + 0i) = Inf + NaNi?

"Gasp!" I know, insane, right? What's going on here? Whatever happened to "anything times one is equal to that same number"? Granted, infinity isn't really a number so sometimes we can't assign a value to an expression like Inf*0, but deep down inside I can't shake the feeling that 1 * Inf really should be Inf!

It turns out that R and I are both right - we're just making different assumptions about how we interpret all these 1s, 0s and Infs in these two statements. Let me explain...

Despite using sound, puppy-approved logic in this case, R gives the offending result because of how it implements everyone's favorite section in Calculus class: computing limits.  To understand why, take a closer look at how the multiplication is happening in each case above.  The first case is hopefully straightforward.  In the second case 1 is treated as a complex number instead of a scalar which gives 

1*(Inf+0i) = (1+0i)*(Inf+0i)  =           

           = Inf + (0*Inf+0)i = Inf + NaNi

We could also throw in a third case and multiply these two complex numbers in the more natural context of polar coordinates. Writing each in terms of their modulus r (distance from the origin) and argument θ (angle off of the positive real axis) instead of in terms of their real and imaginary parts, we have

   1*(Inf+0i) = (1+0i)*(Inf+0i)       

             = 1exp(i0)* Inf exp(i0)

        = (1*Inf) exp (i0)

   = Inf exp(i0)

= Inf + 0i

Whew! So what's "wrong" with multiplying things in x+yi form??

R recognizes that any computations involving infinity really require the algebra of limits, and acts appropriately (albeit conservatively) to evaluate such expressions. This discord then comes from what R assumes is the result of taking some limit and what is to be treated as a constant. Unless you've taught a calculus class recently some explanation might be in order.

In general, expressions involving infinity are treated as limits where some unspecified variable is going to infinity:  For example, statements like Inf*0 can't be assigned a value because in it's most general interpretation we're asking "What is the limit of the product of x*y as x→Inf and y→0?"  Here, whether y goes to 0 from above (e.g. y=1/x) or below (y=-1/x) or neither will determine where the limit of the product goes to zero, some non-zero number, plus or minus infinity, or will have no limit at all. (Open any calculus text to the sections on limits for examples leading to these different outcomes).  Note this example does have an answer if y is always assumed to be 0, since it's always the case that x*0=0.

That means that, depending on how we interepret the zero, our example might equal either

  Inf*0=NaN

Inf*0=0

This is exactly what's going on above.

Returning to the two statements at the top of this post, we can now understand why R gives these two different answers.  By making the zero implicit vs. explicit R treats these expressions differently. R interprets Inf as "the limit of x + 0i as x→Inf," allowing for the result that

1 * Inf = Inf

whereas in the second case R treats Inf + 0i as "the limit of x + yi as x → Inf and y → 0" which has no general answer  and therefore gets assigned a value of NaN.

The take-home message: as soon as there's an Inf in an expression, R proceeds assuming everything is a limit, even though it might be clear to the user that some of those key 1s and 0s should be treated as constants.

Data Visualization in R: Part... 0

I haven't forgotten that I promised to do a series of posts on data visualization using R - just a bit busy catching up after some excellent holiday R&R. Hopefully I'll get a post out soon!

In the mean time, check out these two posts from the R-bloggers network.

Data Visualization: 200 Years of Health and Wealth

This video is super awesome!  It's part of BBC 4's program The Joy of Stats and you can learn a little more about the data here or play with it using this web app on http://www.gapminder.org/. Now don't you wish you could do that with data?

The reason I wanted to share this video (beyond the fact that it's so amazingly awesome) is to let you in on a little secret... are you ready? Here it comes...

Data visualization is easy, and anyone with a computer can do it!

Seriously, it is not that hard! YOU can make cool little wobbling bubble graphs just like in the video! Aren't you excited to learn how?! Yeah? Fantastic!

Now that you're all psyched to visualize some data, I should mention that I am being a bit misleading here... because it does require a bit of computer know-how, and sometimes (ok, almost always) takes a bit of tinkering with the data to find the best ways of boiling down to just the relevant information. But frankly, these things aren't all that hard to learn and aren't always necessary if we're just poking around to get a feel for the data, so none of these words of caution should give you much pause.  Add to that the fact you can always hit up the internet for examples to download and use study and learn from and many of these obstacles are reduced to mere speed bumps.  If you've got a computer, we can get it to plot some data.

Figure 1. Tourist hot spots based on Flickr data. #1 of flowingdata's Top Ten Data Visualization Projects of 2010.

So here's the deal... there are some really cool data available from http://www.gapminder.org/, and I'm going to have a little free time these next few weeks in between birding trips, visiting family and friends, and doing thesis work.  Assuming that free time stays free, I'm going to walk through an example or two of plotting some of this data in R.  If you'd like to follow along, you'll need to download and install R on your computer, and if you don't already have software that can open excel spreadsheets, you'll also want to install something (free) like OpenOffice.

Sound good? Excellent!  Feel free to share any questions or suggestions in the comments section below.  Now hurry along and go install R!

Fast and Sloppy Root Finding

Disclaimer: While the approach to root finding mentioned below is both slow and imprecise, it's also a cheap and incredibly handy approach when all you need to do is get "close enough". If you like R quick and dirty (hey now, get your mind out of the gutter...) this is totally the root finding method for you!

I just read a post on Root Finding (original here) by way of R-bloggers.com which was timely given that only yesterday I'd needed to do some root finding in R to make a figure for a manuscript -- something like the following image.

The blog post prompted me to mention here how I did my root finding for two reasons:

1. Precision and computation time sometimes don't matter all that much; and
2. The way I did my root finding was way easier to implement than convergence-based methods described in the post above.

So here's what I was aiming for, and how I implemented it in R.

The Task: Suppose you're plotting two curves (say, y=f(x) and y=g(x)) and would like to indicate their intersection with an empty circle (i.e. pch=21). In my case, the intersection of these two curves was equilibrium point for a dynamic model, and I wanted to indicate it as such.

If you can find their intersection mathematically (i.e. set f(x)=g(x) and solve for x) then awesome -- do that if you can.  But if for some reason you can't, and you know a single root exists in some interval a≤x≤b, you can find that root quickly using some straightforward vector tricks.

The Solution: Lets use the example of finding the intersection of f(x) = x/(1+x) and g(x) = (5-x)/5 over the interval (0,5).

Step 1:  Define an x vector full of values between a and b.  The smaller the step size (or, the longer the list) the better.

> x = seq(0, 5, length=5000);

Step 2: Compute the square of the difference of your two functions over that interval using x.  This is as simple as the line of code...

> fgdiff = ( x/(1+x) - (5-x)/5 )^2;

Step 3: Using the which() function, we can pick out the index for the smallest value in our list of squared differences... Once we know this index (call it j) we know the intersection occurs at, or very near, the x value x[j], and we're basically done! 

> j = which(fgdiff==min(fgdiff))[1]; 
> j; x[j];  ## show the value of j, x[j]

For a closer look at what's going on with that which() statement, check out the help for which() and following example.

## A Closer look at the which(fgdiff==min(fgdiff))
> ?which
> which(c(F,F,T,T,F))
[1] 3 4
> which(c(F,F,T,T,F))[1]
[1] 3
> xample = c(5:1,2:5); xample
[1] 5 4 3 2 1 2 3 4 5
> min(xample)
[1] 1
> xample==min(xample)
[1] FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE
> which(xample==min(xample))
[1] 5
> which(xample==min(xample))[1]
[1] 5

Step 4: Since both functions are (approximately) equal at this x value, it only remains to decide whether you want to indicate the point of intersection using (x, f(x)) or (x, g(x)).

> points(x[j], x[j]/(1+x[j]), pch=19, cex=2)

All done!

If you'd like to tinker with this example, here's the code to produce the image above.

The Math Behind Morphing Faces: Linear Algebra

Animations of morphing faces or combinations of multiple images into one can be quite a thing of beauty.  But how exactly are those photos so carefully blended together? 

While the answer to that question is beyond the scope of what I could put into a single blog post, understanding that answer requires some basic knowledge of one very important are of mathematics: linear algebra.  It's important not just for the number-crunching tools it provides, but because it helps us think about things differently and know how to ask the right questions and know whether or not those questions have answers.  Before I get too far ahead of myself lets first take a look at the video which motivated this post in the first place, which strings together 60 years of female actors from CBS (click the button in the lower right corner to watch it full-screen):

CBS - 60 Years of Actresses from Philip Scott Johnson on Vimeo.
More videos by Philip Scott Johnson (including CBS -
60 Years of Actors) can be found on vimeo and on youtube.

So how are these animations created?

If you replay part of the video, you'll notice that there are two things going on: 1) facial features in each image are stretched and rotated to line up with the facial features of the next image, and 2) there's a fade from one image to the next. The fade seems simple enough, so lets just focus on the first process of stretching and rotating facial features.

Home birth death toll rising in Colorado?

Dr. Amy Tuteur, the Skeptical OB, has a blog post up entitled 'Inexcusable homebirth death toll keeps rising in Colorado.'  Now I'm a big fan of science-based medicine (and of Tuteur's blog), however I have to call foul when it comes to that "rising" part of her post.  Yes, I think it's pretty minor point since the real comparison to consider is the home birth vs. hospital birth mortality rates - but this is a nice opportunity to do some basic stats. Having left a few comments to that effect on her blog, I figured I would summarize them here.

R Tip: Listing Loaded Packages

A friend recently asked how you list the packages currently loaded into R's workspace, as opposed to listing all available packages which is what library() does. The answer?

> (.packages())

Paul Pick's Spain

I don't follow professional sports much, so I was a little confused to read on Jerry Coyne's blog that apparently I had chosen Spain, and that Jerry agreed.  Then I realized he was of course talking about Paul the cephalopod, not Paul the grad student who should be writing his thesis right now instead of blogging.

Despite the fact that I'll be content to see either country win, Jerry was right!  I really did end up picking Spain!  I didn't have an octopus handy, and no coins within reach of my computer, so I just used R to do the coin toss. See for yourself...

> date()
[1] "Fri Jul 09 12:09:24 2010"
> set.seed(09072010)
> ifelse(runif(1) <= 1/2, "Spain", "Netherlands")
[1] "Spain"
> 

See, Spain wins!  Wow - I mean really, what are the odds?

Software for Science & Math (part II): Getting started with R

A while back I wrote the first post in a series where I'll cover important concepts from Calculus, Probability and Statistics that (IMO) everyone should be familiar with. I wanted to occasionally involve two free software platforms (R and Maxima) in those posts, and I've finally gotten around to a post dedicated to getting started with R.

R is a handy computing platform and great way to learn basic programming skills. It can do basic statistics, plot data or mathematical functions, and provides access to a menagerie of advanced tools via R packages. And, it's all free. R's broad functionality and statistical capabilities makes familiarity with R a valuable skill in the natural sciences.

Getting Started with R

If you haven't already installed R on your computer you should check out this website on downloading and installing R or you can just pick your nearest CRAN mirror (e.g. at UCLA, NCI in Maryland, etc.) and download and install the appropriate version per their instructions.  If the install isn't working, feel free to post questions in the comments below.

Basic Interactive Examples

Software for Science & Math: R and Maxima (part I)

In the coming months, I plan to write a series of posts reviewing "must-know" mathematics everyone should be familiar with: important concepts from Calculus, Probability and Statistics.  Here I begin by introducing some free software you can use to follow along, or use for your own computational tasks. In future posts, I'll encourage a little hands-on learning of these applications by providing code and other information so you can recreate my figures and results. 

Science has emerged as humankind's most effective way of understanding reality.  The success of the scientific method is largely a product of two key components: (1) a strong reliance on empirical data, and (2) a precise and powerful theoretical framework to properly formulate hypotheses, make predictions about experimental outcomes, etc.

Skipping over the importance of data (for now), I'd like to introduce some computational tools that you might consider installing on your computer. The applications are the computing platform known simply as R, and the software for doing symbolic manipulations (e.g. algebra) known as Maxima. I should mention this software isn't just for goofing around and writing blog posts -- these applications can be used to do research-level mathematical, statistical and numerical work. So you may find on or both to be valuable assets.

Oh, right -- and did I mention they're both free?

Dividing by zero

A friend of mine requested I do a post about diving by zero... and recalling this image I just couldn't resist!

While mathematicians publicly cringe at the idea of such divisions, we don't really worry too much about them in practice... they're easy enough to avoid and when the problem does arise, well -- we have our tricks! 

So what happens when you divide by zero? Broadly speaking, a few things can happen. No, the universe won't explode or anything like that, although you can do fun tricks like "prove" that 1=2 (see below).

What really happens -- if you're just dividing a number by zero -- is the outcome is undefined.  Not a number. No solution.  It's nonsense.  Nothing interesting happens.   But suppose you divide by almost zero? Then what?  Can we learn anything about these "almost zero" cases?

It turns out we can, and the mathematical tools used to do so turn out to be fundamental to our ability to use math to understand real-world processes.  To understand all this, however, we need to begin by thinking about such divisions in the context of functions.

Suppose you have two functions f(x) and g(x) -- that is, two curves like the ones shown above -- and you make a new curve h(x) = g(x)/f(x) that is their ratio.  If the denominator f(x) is somewhere equal to zero -- in our example, at x=0 and x=1 -- then what happens for nearby values of x?

At this point, we're doing homework straight out of a first course in Calculus.  To do this properly, we'd draw on one of the most useful tools in mathematics -- the notion of limits -- which allow us to formalize some otherwise intuitive ideas and develop a ton of really useful tools for understanding more complicated looking functions (tools like, oh, say... all of calculus).

Without going into the mathematical details, these allow us to obtain precise (and often very general) statements similar to the following statements about our function h(x).

First, we know h(x)  is undefined at x=0 and x=1. If we ask what happens to values of h(x) close to x=0, we begin to learn something more about h(x) which, in some applications might be the answer to an important question.  Here, lets take a look at our toy example as define above.

Graphically, we can see that as x nears 0 from either direction, h(x) nears negative infinity.  In this case, we'd say the limit as x goes to zero is negative infinity.  On the other hand, as we consider x values near 1 we see that h(x) either runs off to negative infinity (x<1) or positive infinity (x>1).  In this case, as the limit goes two different directions depending on whether you approach x=1 from above or below. In this case we say that at x=1, the limit does not exist.  The usual pre-calculus questions about limits of (mostly) continuous functions.

So what does any of this have to do with dividing by zero?  After all, graphically this all seems a bit pointless!

It turns out that the problem of dividing by zero is the comical counterpart to some of the most powerful and ubiquitous tools in mathematics. The same properties of limits used to derive results like those above (from equations, instead of graphs) are the same concepts that provide a foundation for scientific theories in engineering, statistics, biology, chemistry, physics, and medicine.

A great place to build a foundation for understanding and using those tools is with a little bit of calculus, probability and statistics - any one of which would require more than another post or two, but might be well worth doing.

Until then, if you'd like a little calculus refresher there are a handful of free resources online including those here, here and here (all three of which are reviewed here).

As always, suggestions and requests can be shared via email or in the comments below.

R code for the figures above: 

How to make pi ... using R

There's another irresistible post over at Dot Physics, this time on a nifty way to estimate the value of pi using random numbers. Check out that post for details, then hop back over here!

(brief pause...)

Ok, you're back! And you loved the post - awesome.  But didn't it feel like it was lacking a little... pie?  I too had the very same feeling, so I wrote my own version of Rhett's simulations (using R) but with some fanciful graphics just to jazz things up a bit.

Figure 1: The fraction of points that fall "on the pie" (left) give a reasonable 

approximation of π=3.14159... Lines on the right show π and our estimate.

If you have R installed on your computer, run the code below for the animated version.

R, I still love you, but I hate your round() function!

You all remember the concept of rounding, right? I first learned to round numbers by taking them to the nearest integer (e.g. rounding 2.1 gives 2, rounding 3.9 gives 4, and so on) and in cases like 2.4 -- rounding up to the nearest integer.  I'll admit that as a child I didn't always pay attention in math class, but I was a bit surprised to learn recently that there are a number of different rules for rounding (and that being unaware of this fact can totally ruin your day).

How I came to choose this topic to blog about first requires sharing the following story... which I'll preface with a little background.

Dr. Wife and I both do work related to mathematical biology, and frequently use computers to tackle some of the more unruly bits of math we encounter.  Computer software for doing mathematics can roughly be divided into two main categories: The numerical software that crunches numbers  (not a technical term, I just like calling them number crunchers), and the computer algebra systems (or CASs).  This later variety do symbolic (or algebraic) manipulations like reducing fractions, and working with xs and ys instead of numbers.

For example, if you wanted to find a formula for the integral of 

x^2+sin(x) from x=a to x=b, 

software like Maple, Mathematica or the free software Maxima would tell you the answer is  

cos(a)-cos(b)-(a^3-b^3)/3.

If it involves symbols, and algebraic manipulations - you want a CAS!

Now,if you just wanted to do something like plot data, generate random numbers or do statistical work -- computations using explicit numbers not just symbols -- then you'd want to use software that excels at crunching numbers.  Something like Matlab, Octave, R or programming languages like fortran, C, or python (just to name a few).

Quick tangent: while I'm a fan of Maple and Matlab, they cost money.  Enough  money that I'd rather use free alternatives when I can, especially if I might want to share my code with friends or collaborators but don't want them to spend money just to run it. Anyway, that's my plug for Maxima (a CAS) and R (statistical software that is also a great alternative to Matlab) -- but lets get back to the story...

The other day, Dr. Wife and I were working at home. She had a bug in some R code that -- after much hair-pulling -- was finally attributed to the following unexpected behavior of R's round() function:

> x = c(1, 1.5, 2, 2.5);
> rbind(x=x, round = round(x));
      [,1] [,2] [,3] [,4]
x        1  1.5    2  2.5
round    1  2.0    2  2.0
> 

Notice there's something weird going on here... 1.5 gets rounded UP to 2 (as it should, if you think of rounding like most Americans), but 2.5 gets rounded DOWN to 2! What's going on with the round() function in R?!  Just to make sure I wasn't screwed over by all of my math teachers, I also checked in Matlab which gave the expected result...

> x=[1 1.5 2 2.5];
> [x; round(x)]
ans =
    1.0000    1.5000    2.0000    2.5000
    1.0000    2.0000    2.0000    3.0000
>

So what's going on here???

Quoting the wikipedia page on Rounding, there are different ways to round numbers depending on the task at hand...

1. round to nearest: q is the integer that is closest to y...
2. round towards zero (or truncate): q is the integer part of y, without its fraction digits.
3. round down (or take the floor): q is the largest integer that does not exceed y.
4. round up (or take the ceiling): q is the smallest integer that is not less than y.
5. round away from 0: if y is an integer, q is y; else q is the integer that is closest to 0 and is such that y is between 0 and q.

Sadly, my favorite number crunching software (that would be R) uses one of the dumbest rules out there (well, dumb from a mathematical perspective) to decide what to do with numbers ending on ".5".  Both R and Matlab use the "round to the nearest neighbor" rule -- but the way they deal with the half-way point turns out to be the the source of the discrepancy above.

In school, most of us learned this rule (again, from the wikipedia page on Rounding):

Round half up

The following tie-breaking rule, called round half up, is widely used in many disciplines:

• If the fraction of y is exactly .5, then q = y + 0.5

That is, half-way values y are always rounded up. For example, by this rule the value 23.5 gets rounded to 24, but -23.5 gets rounded to -23...

This is what Matlab does, and is what most people think of when they round numbers.

The numerical routines in R implement a different rule (italics added for emphasis):

Round half to even

A tie-breaking rule that is even less biased is round half to even, namely

• If the fraction of y is 0.5, then q is the even integer nearest to y.

Thus, for example, +23.5 becomes +24, +22.5 becomes +22, -22.5 becomes -22, and -23.5 becomes -24. This variant of the round-to-nearest method is also called unbiased rounding, convergent rounding, statistician's rounding, Dutch rounding, Gaussian rounding, or bankers' rounding...

That's right -  R rounds to even.  Yes, it's primarily a stats platform. Yes, this is all explicitly stated in the documentation for the round() function, and of course I still love R, but seriously -- round to even?  To make matters worse, that day we also had other bugs that were essentially caused by the fact that (in both Matlab and R)

> (0.1+0.05) > 0.15
[1] TRUE 
>

So what's the moral of the story?  Well I'm not quite sure yet ... I still like R, and I certainly will continue to use it.  I'll probably end up reading through the documentation for frequently used functions -- not just unfamiliar functions -- and as much as I'd like to pretend it doesn't matter,I'll certainly keep an eye out for ways my code might get sabotaged by round-off error.

Shame on you, R...

... as such a fine, upstanding free software package that allows one access to all the latest statistical methods and modeling packages, you really should know better than to go about telling people that

> 1/0
[1] Inf