All this made me wonder about the issue of dimensionality in trying to understand "a billion". Let me explain...
Previously, I'd come up with my own way of thinking about "1 billion years" in terms of distances. This was all in the context of thinking about "deep time" when it comes up in geology and evolution (that post is here). After all, today, people get to travel quite large distances pretty easily, yet we can also appreciate the idea of small distances like centimeters and millimeters.
That's how the question of dimensionality came up. The grid above is a two-dimensional grid. In contrast, my distance example is a one-dimensional illustration of "a billion". So does dimensionality matter? Does it matter whether we're thinking about "a billion" in terms of a length, an area or a volume?
I haven't quite worked out an answer yet, but I think it does. To illustrate this fact,
it helps to consider comparable illustrations of "a billion" starting with distance.
Using millimeters as the base unit, a kilometer is 1,000,000 millimeters, making a billion millimeters 1000 km -- an appreciably large distance (1000 km ~= 621.4mi). If you counted all those millimeters, one second at a time, it would take about 32 years to finish, in case you were curious.
Fig 1: 1 billion mm = 1000km (~621.4mi) courtesy of Google Earth.
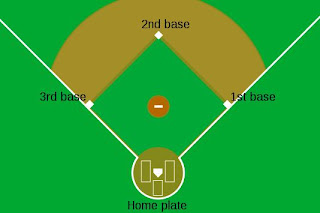
While the grid of dots is pretty cool for thinking of a 2D image of "a billion", lets extend our linear example to an area. Consider units of millimeters squared - an area given by a 1mm-by-1mm square. A billion of these covers an area that is about sqrt(1000000000mm^2) ~= 31.623m x 31.623m plot of land. That is a square area that has dimensions 0.02 x 0.02 miles, or about 35x35 yards... so roughly the size of the interior area of high school baseball diamond.
Fig 2: Inside the bases = 1 billion mm2, about 31x31 m2.
3D? Sticking to mm for now, a mm cubed is a microliter. This gives a volume (of water?) that is a cube with dimensions of 1000mm, or a cubic meter of water. If we used mL instead of microL? That would fill a 10m x 10m x 10m cube, about the size of a small pond.
Fig 3: A cubic meter = 1 billion mm3. A 10-by-10-by-10 stack of these is a billion mL.
So how big is a billion?
Using units of millimeters (depending on whether they're linear, squared or cubed millimeters...) a billion is equivalent to a distance of 600+ miles, the interior of a baseball diamond, or a single cubic meter of water.
Thoughts?








1 comments:
I think Earth has a human/rodent problem!
Very intersting to have things put into perspective like that :)
Post a Comment